Notice that:
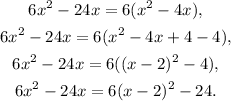
Therefore, f(x) has an absolute minimum of -24 at x=2.
Since the given function is a parabola (in the interval [0,5]) with a leading coefficient greater than zero and vertex at (2,-24) we get that it has an absolute maximum at x=5, which is:
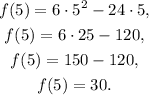
Answer:
Absolute maximum=(5, 30).
Absolute minimum=(2, -24).