The function given is:
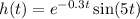
To find the first derivative, we need to use several rules of differentiation.
One of them is the chain rule.
Given two functions f(x) and g(x), the chain rule is:
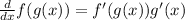
Next, the derivative of the exponential:
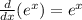
The derivative of the product:
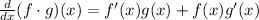
And the derivative of sine and cosine:
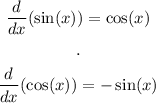
Now, we can break the function into pieces. First we have:
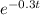
The derivative is, by the chin rule:
:
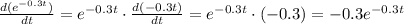
Next:
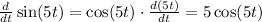
Then, we can write:
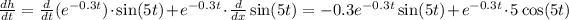
We can simplify:
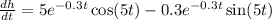
Now, for the next derivative, we can separate the terms:
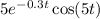
And differentiate:
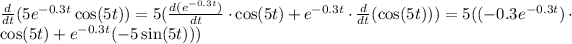
We can simplify:
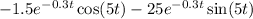
The other term of dh/dt is:
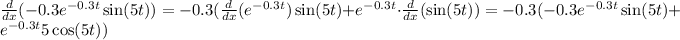
Simplify.
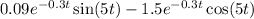
Thus:
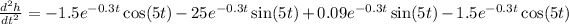
We can simplify:
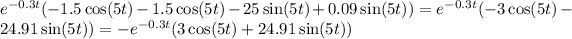
The answer is:
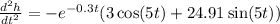
Finally, the second derivative of a position function represents the acceleration, thus:
The correct measurement unit for the second derivative is: cm/sec^2
Answers:
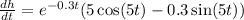
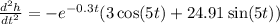
The correct measurement unit for the second derivative is: cm/sec^2