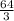Question

How do I determine the sum of the infinite series

Answer 1

Given the geometric series below;

`S\infty=16+4+1+\cdots`

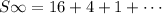
Note the following;

`a_1=16,r=(1)/(4)`

The common ratio r, is derived as follows;

`\begin{gathered} r=(4)/(16),r=(1)/(4) \\ \text{Therefore,} \\ r=(1)/(4) \end{gathered}`

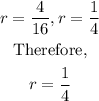
To calculate the sum of the infinite geometric series, we shall use the formula given as;

`S\infty=(a_1)/(1-r)`

Note that this would only apply if;

`\begin{gathered} r<1,r\\e0 \\ \text{Also, the common ratio must be an absolute value. } \\ |r|<1,r\\e0 \end{gathered}`

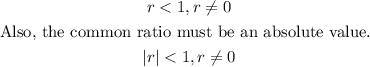
We can now solve the sum as shown below;

`\begin{gathered} S\infty=(a)/(1-r) \\ S\infty=(16)/(1-(1)/(4)) \\ S\infty=(16)/((3)/(4)) \\ S\infty=(16)/(1)\text{ / }(3)/(4) \\ S\infty=(16)/(1)*(4)/(3) \\ S\infty=(64)/(3) \end{gathered}`

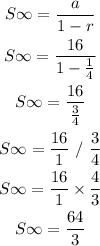
ANSWER:

The correct answer is option B;

`(64)/(3)`