Question

a. Tell whether the model represents exponential growth or exponential decay. b. Identify the annual percent increase or decrease in the value of the bike. c. Estimate when the value of the bike will be $50.

Answer 1

we have the function

`y=200(0.75)^t`

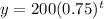
In this problem, we have an exponential decay function because the value of the base of the exponential function is less than 1

b=0.75

b< 1 -----> exponential decay function

Part b

Find out the annual percent decrease

b=0.75

b=1-r

0.75=1-r

r=1-0.75

r=0.25

r=25%

therefore

The annual percent decrease is 25%

Part c

For y=$50

substitute in the given equation

`50=200(0.75)^t`

Solve for t

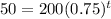
`(50)/(200)=(0.75)^t`

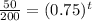
Apply log on both sides

`\log ((50)/(200))=\log (0.75)^t`
`\log ((50)/(200))=x\cdot\log (0.75)`

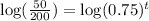
x=4.8 years