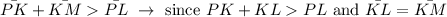1. Firstly, statement 1 is given in the question.
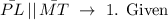
2. When two lines cut through two parallel lines, the alternate interior angles are congruent(equal)
So;
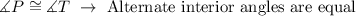
3. Given
4. PK = KT
Since K is the mid point of PT as stated in the question, then PK will be of equal length as KT.
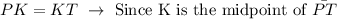
5. Vertically opposite angles are equal.
So;
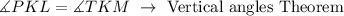
6. when two corresponding angles and the included side are respectively equal, a triangle is said to be congruent.
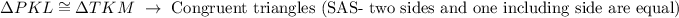
7. The Triangle Inequality theorem states that the sum of two sides of a triangle is greater than the third side.
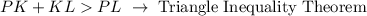
8. CPCTC means that Corresponding Parts of Congruent Triangles are Congruent.
The corresponding sides of the two congruent triangles are;
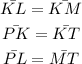
So;
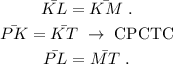
9. The final one is a conbination of CPCTC and Triangle Inequality theorem