Question

Find and solve a and b then verify the function

Answer 1

Hello!

We have the function f(x) = 3x.

The first step is to calculate the inverse function of f(x):

First, let's replace where's f(x) by y:

f(x) = 3x

y = 3x

Now, let's swap the values of x and y:

y = 3x

x = 3y

Now we have to solve it to obtain y:

3y = x

y = x/3

So, we will have:

`f(x)^(-1)=(x)/(3)`

B. Reasoning:

`\begin{gathered} f(f^(-1)(x))=(3((x)/(3))=x \\ \\ f^(-1)(f(x))=(3x)/(3)=x \end{gathered}`

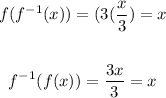
Image with the reasoning:

So, these equations are correct.

As it has no restrictions, this function is valid for all values of x.

Right answer: alternative A.

Obs: You'll have to type in the first box: x/3.