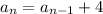Answer:
The recursive formula for the given sequence is;
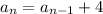
Step-by-step explanation:
Given the sequence;
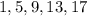
The sequence above is an Arithmetic Progression AP.
Writing the recursive formula;
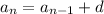
for the sequence, the common difference d is;
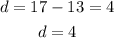
The recursive formula will then be;