ANSWER
![6\operatorname{cm}]()
Step-by-step explanation
First, let us make a sketch of the circle:
Since the diameter of the circle is 20 cm, the radius of the circle is 10 cm, as shown above.
The two radii and the chord of the circle form a triangle. Also, the distance from the center to the chord forms a right triangle with the radius and half the length of the chord:
Now, we can solve for d by applying the Pythagoras theorem:
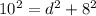
Solve for d:
![\begin{gathered} d^2=10^2-8^2 \\ d^2=100-64=36 \\ d=\sqrt[]{36} \\ d=6\operatorname{cm} \end{gathered}]()
That is the distance from the chord to the center of the circle.