Given: The quadratic equation below
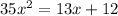
To Determine: The two linear factors of the given equation using standard form of a quadratic equation
The standard form of a quadratic equation is given as

Re-write the given equation in the standard form as shown below
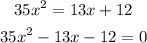
Factor the left hand side as shown below
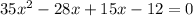
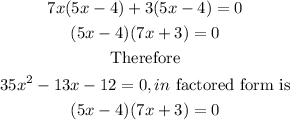
Hence, the two linear factors of the given equation is
(5x -4)(7x + 3) = 0