Question

(Find the sum of the infinite geometric series 3 + 12 + 48 + 192 + ...

Answer 1

Given the Infinite Geometric Series:

`3+12+48+192+...`

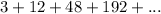
You can find its sum by using this formula:

`S=(a_1)/(1-r)`

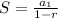
Where "r" is the common ratio and the first term is:

`a_1`

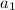
In this case, you can identify that each term is obtained by multiplying the previous term by 4. Therefore:

`r=4`

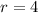
You can identify that:

`a_1=3`

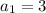
Therefore, you can substitute values into the formula and evaluate:

`S=(3)/(1-4)`
`\begin{gathered} S=(3)/(-3) \\ \\ S=-1 \end{gathered}`

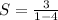
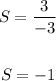
Hence, the answer is: Option B.