ANSWER
Account A = $96.80
Account B = $48.40
Step-by-step explanation
We have that in the two accounts A and B, $1000 is invested.
We want to find the simple interest earned by the two accounts. To do this, we apply the formula for Simple Interest:
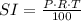
where P = principal (amount invested)
R = rate
T = amount of time
ACCOUNT A
It earns simple interest at a rate of 2.42% over 4 years.
Therefore, the simple interest earned is:
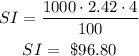
ACCOUNT B
It earns simple interest at a rate of 2.42% over 24 months. For this, we have to divide by 12 months (since the formula is originally for year).
Therefore, the simple interest earned is:
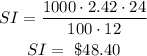
We have calculated the Simple Interest for both accounts.
We see that the simple interest for Account A is twice that of Account B. This is simply because Account A earned for twice the amount of time that Account B earned for.