Given the function:
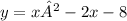
we have that the factored form is:
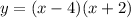
with this representation, we can see that the x-intercepts are:
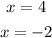
Next, the axis of symmetry can be found with the following expression:

in this case, a = 1 and b = -2 (since a and b are the main coefficients on the equation), then, the axis of symmetry is:
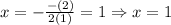
The vertex can be found by evaluating the axis of symmetry on the equation. then, if we make x = 1, we get:

therefore, the vertex is the point (1,-9).
Finally, the domain of the function is the set of all real numbers (-inf,inf), since it is a polynomial function. The range is [-9,inf), since the vertex is located at the point (1,-9)