We have a point A=(7,-3) that is reflected over point C=(6,-5). This means that is refected in an axis that is perpendicular to the segment AC.
The image is point B, and we need to calculate its coordinates.
We can relocate the center of coordinates to point C, do the reflection and then relocate the original center of coordinates.
If now C became the center of coordinates A becomes:
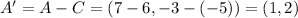
Now, we can reflect it as normal:
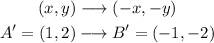
Now, we convert this to the original coordinates as:
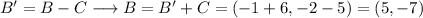
The point B is (5,-7).