Let the formula be for time in seconds
Thus, we have:
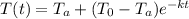
T_a would be the freezer temperature, 4
T_0 would be the initial temp, which is 73
t is the time [9 minutes afterwards, t = 9]
k is 0.05
Substituting, we get:
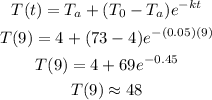
To nearest degree Fahrenheight, T = 48 degrees F