Question

Find the equation of the linear function in STANDARD form.

Answer 1

It is required to find the equation of the given line in standard form.

Recall that the equation of a line in standard form is written as:

`Ax+By=C`

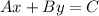
Where A, B, C are constants.

The Equation of a line with a slope, m that passes through the point (x₁,y₁) in Point-Slope form is given as:

`y-y_1=m(x-x_1)`

The slope formula for a line that passes through points (x₁,y₁) and (x₂,y₂) is given as:

`m=(y_2-y_1)/(x_2-x_1)`

Notice from the graph that the line passes through points (2,0) and (4,5).

Substitute (x₁,y₁)=(2,0) and (x₂,y₂)=(4,5) into the slope formula to find the slope:

`m=(5-0)/(4-2)=(5)/(2)`

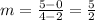
Substitute m=5/2 and the points (x₁,y₁)=(2,0) into the point-slope form of the equation of a line:

`\begin{gathered} y-0=(5)/(2)(x-2) \\ \Rightarrow y=(5)/(2)x-(5)/(2)(2) \\ \Rightarrow y=(5)/(2)x-5 \end{gathered}`

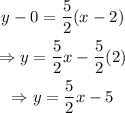
Next, rewrite the equation in the standard form of the equation of a line:

`\begin{gathered} y=(5)/(2)x-5 \\ \Rightarrow y-(5)/(2)x=-5 \\ \Rightarrow-(5)/(2)x+y=-5 \end{gathered}`

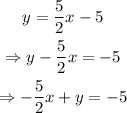
The required equation in standard form is -5/2 x+ y = -5.