Part a.
The break-even point is where the cost equals to the revenue, that is,
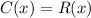
Then, by substituting the given information, we get
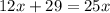
So, by subtracting 12x to both sides, it yields,
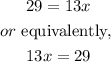
Then, x is given by
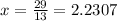
Then, by rounding to the nearest whole number, the break even quantity is 2 medals.
Part b.
The profit is equal to the revenue minus the cost, that is,

So we have
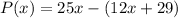
which gives
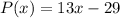
By substituting x=25o into this result ,we have
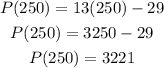
Therefore, the profit from 250 units is $3221.
Part c
In this case, we need to substitute P=130 into the profit function and find x, that is,
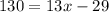
So, by adding 29 to both sides, we have
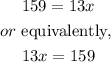
Therefore, we have

Therefore, by rounding to the nearest whole number, the number of medals to produce a profit of $130 is 12 medals.