(a)
Let Wj be the wages of John and Tj be the time in hours.
If wages and time are proportional, then the relation between them can be expressed as,
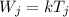
Here, k is a constant
Rewriting the above equation,

If the ratio of wages to hours is a constant, then the wages of John is proportional to time.
Taking the ratio of Wj to Tj, we get

Since the ratio of wages to time is a constant, John's wages are proportional to time.
The constant k is the the unit rate. Therefore, the unit rate at which John works is $9/h.
(b)
The graph plotted with Amber's wages against hours worked is a straight line. Therefore, Amber's wages are proportional to time.
The slope of the graph gives the unit rate.
Hence, the unit rate at which Amber work is given by,
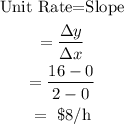
Therefore, the unit rate at which Amber work is $8/h