Question

Find the coordinates of the other endpoint of the segment, given its midpoint and one endpoint. (Hint: Let (x,y) be the unknown number endpoint. Apply the midpoint formula, and solve the two equations for x and y. midpoint (-6, -20), endpoint (-4,-16)The other endpoint is___(Type an ordered pair.)

Answer 1

Given the coordinates:

midpoint(-6, -20)

Endpoint 1(-4, -16)

To find endpoint 2, apply the midpoint formula below:

`x_{m,\text{ }}y_{m\text{ }}=\text{ (}(x1+x2)/(2),\text{ }(y1+y2)/(2))`

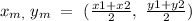
Where,

(xm, ym) = (-6, -20)

(x1, y1) = (-4, -16)

(x2, y2) = unknown

Let's find the mising coordinates (x2, y2)

`\begin{gathered} \text{For x2:} \\ -6\text{ = }(-4+x2)/(2) \\ \\ -12\text{ = -4 + x2} \\ \\ x2\text{ = -12 + 4} \\ \\ x2\text{ = -8} \end{gathered}`
`\begin{gathered} \text{For y2:} \\ -20\text{ = }(-16+y2)/(2) \\ \\ -40\text{ = -16 + y2} \\ \\ y2\text{ = -40 + 16} \\ \\ y2\text{ = }-24 \end{gathered}`

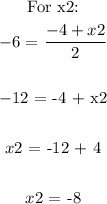
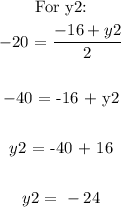
Therefore, the other endpoint is (-8, -24)

ANSWER:

(-8, -24)