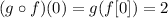Question

Let g(x) = 3f(x) - 7. Find g(0). What does this point represent?

Answer 1

To find g(0), you can see what happens to f (x) when x = 0. So, if you look at the graph of f (x), you can see that if x=0, f(0) = 3, then

`\begin{gathered} g(x)=3f(x)-7 \\ g(0)=3f(0)-7 \\ g(0)=3(3)-7 \\ g(0)=9-7 \\ g(0)=2 \end{gathered}`

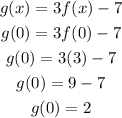
Now, this point represents the result of performing the composition of functions

`(g\circ f)(x)=g(f\lbrack x\rbrack)`

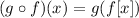
Where g(x)=3f(x) - 7 and f(x) is function graphed, and evaluating at x = 0, that is

`(g\circ f)(0)=g(f\lbrack0\rbrack)=2`