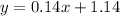ANSWER:
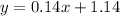
Explanation:
We have that the equation in its slope and intercept form is the following
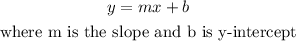
We calculate the slope with the following formula

We replace the following points (102, 15.5) and (130, 19.3)
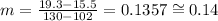
Now we calculate the value of b, knowing the slope and the point (102, 15.5)
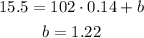
Therefore, the closest equation is: