Question

What is the future value of $2000 earning 12% interest, compounded monthly, for 6 years? (Round your answer to two decimal places.)

Answer 1

The formula for compounded interest is as follows:

`A=P(1+(r)/(n))^(nt)`

Where A is the final amount, P is the principal amount (the initial amount), r is the annual interest rate, n is how many times it is compounded per year and t is the time in years.

We already have:

`\begin{gathered} P=2000 \\ r=12\%=0.12 \\ t=6 \end{gathered}`

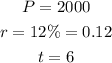
Also, we know that it is compounded monthly. Since there are 12 month per year, each ear it will be compounded 12 times:

`n=12`

Now, to get the final amount, we just need to substitute this values and evaluate:

`\begin{gathered} A=P(1+(r)/(n))^(nt) \\ A=2000(1+(0.12)/(12))^(12\cdot6) \\ A=2000(1+0.01)^(72) \\ A=2000(1.01)^(72) \\ A=2000\cdot2.0470\ldots \\ A=4094.1986\ldots\approx4094.20 \end{gathered}`

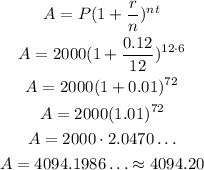
So, the future value is approximately $4094.20.