Answer:
a)
A system of equations representing the scenario is;
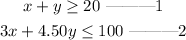
b)
she meets both requirements If she prepared 15 vegan and 10 non-vegan meals. because the total number of meals is at least 20 and the cost is less than $100.
Step-by-step explanation:
Given that each vegan meal cost $3.00, and each non-vegan meal cost $4.50.
Let x represent the number of vegan meals and y represent the number of non-vegan meals.
And there will be at least 20 people attending the party;
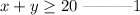
Also, dahlia can spend at most $100 for preparing the meals;
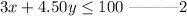
Therefore, a system of equations representing the scenario is;
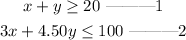
If she prepares 15 vegan and 10 non-vegan meals
We need to confirm if it meets both conditions;
condition 1;
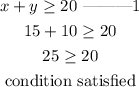
Condition 2;
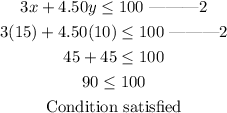
Therefore, she meets both requirements If she prepared 15 vegan and 10 non-vegan meals. because the total number of meals is at least 20 and the cost is less than $100.