Answer:
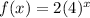
Explanations:
The standard exponential function is given as:

Given the coordinate points (2, 32) and (3, 128)
The two exponential functions will be;
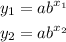
Substitute the given coordinates to have:
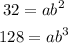
Divide both expressions to have:

Determine the value of "a"
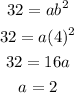
Substitute b = 4 and a = 2 into the original equation to have;
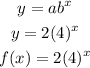
This gives the required exponential function