In the quadratic formula, the expression under the sign of the square root, b^2 - 4ac, is called the discriminant.
If the discriminant is negative, then there are no real solutions to the equation.
If the discriminant is zero, there is only one real repeated solution.
If the discriminant is positive, it means that you get two unequal real solutions.
We have the following quadratic equation:
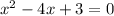
Where:
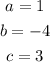
Therefore our discriminant is:
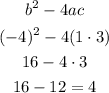
Our discriminant is positive.
In conclusion, the quadratic equation has two unequal real solutions.