Question

Section 5.2 Problem 21:

Solve the initial value problem and graph the solution.

`y'' + 4y' + 10y = 0`

`y(0) = 3`

`y'(0) = - 2`
​

Answer 1

`y(x)=e^(-2x)[3cos(√(6)x)+(2√(6))/(3)sin(√(6)x)]` (See attached graph)

Explanation:

To solve a second-order homogeneous differential equation, we need to substitute each term with the auxiliary equation
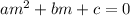`am^2+bm+c=0` where the values of
`m` are the roots:

`y''+4y'+10y=0\\\\m^2+4m+10=0\\\\m^2+4m+10-6=0-6\\\\m^2+4m+4=-6\\\\(m+2)^2=-6\\\\m+2=\pm√(6)i\\\\m=-2\pm√(6)i`

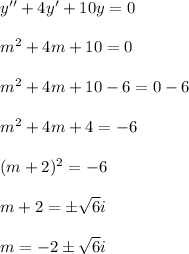
Since the values of
`m` are complex conjugate roots, then the general solution is
`y(x)=e^(\alpha x)[C_1cos(\beta x)+C_2sin(\beta x)]` where
`m=\alpha\pm\beta i`.

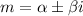Thus, the general solution for our given differential equation is
`y(x)=e^(-2x)[C_1cos(√(6)x)+C_2sin(√(6)x)]`.

To account for both initial conditions, take the derivative of
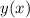`y(x)`, thus,
`y'(x)=-2e^(-2x)[C_1cos(√(6)x+C_2sin(√(6)x)]+e^(-2x)[-C_1√(6)sin(√(6)x)+C_2√(6)cos(√(6)x)]`

Now, we can create our system of equations given our initial conditions:

`y(x)=e^(-2x)[C_1cos(√(6)x)+C_2sin(√(6)x)]\\\\y(0)=e^(-2(0))[C_1cos(√(6)(0))+C_2sin(√(6)(0))]=3\\\\C_1=3`

`y'(x)=-2e^(-2x)[C_1cos(√(6)x+C_2sin(√(6)x)]+e^(-2x)[-C_1√(6)sin(√(6)x)+C_2√(6)cos(√(6)x)]\\\\y'(0)=-2e^(-2(0))[C_1cos(√(6)(0))+C_2sin(√(6)(0))]+e^(-2(0))[-C_1√(6)sin(√(6)(0))+C_2√(6)cos(√(6)(0))]=-2\\\\-2C_1+√(6)C_2=-2`

We then solve the system of equations, which becomes easy since we already know that
`C_1=3`:

`-2C_1+√(6)C_2=-2\\\\-2(3)+√(6)C_2=-2\\\\-6+√(6)C_2=-2\\\\√(6)C_2=4\\\\C_2=(4)/(√(6))\\ \\C_2=(4√(6))/(6)\\ \\C_2=(2√(6))/(3)`

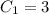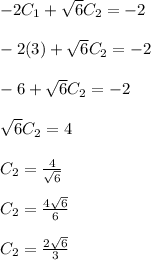
Thus, our final solution is:

`y(x)=e^(-2x)[C_1cos(√(6)x)+C_2sin(√(6)x)]\\\\y(x)=e^(-2x)[3cos(√(6)x)+(2√(6))/(3)sin(√(6)x)]`