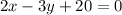Solution:
Given that;
Line 1 passes through the points A(-15,-8) and B(-3,0)
To find the slope, m, of the line, the formula is
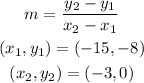
Substituting the coordinates to find the slope of line 1
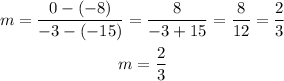
Since, line 3 is parallel to line 1, then, they will have the same slope,
Thus, the slope pf line 3 is 2/3
Line 2 has equation 3x + 2y - 35 = 0.
Where line 3 intersects line 2 at x = 5, substitute for x into the equation of line 2 to find the value of y
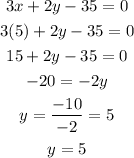
Where
The slope and the coordinates on line 3 are
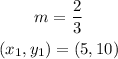
Applying the point-slope formula to find the equation of line 2
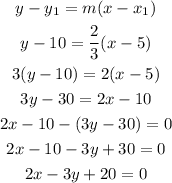
Hence, the equation of line 3 is