Heron's formula makes use of s, which is described as the semi-perimeter of the triangle. Before we can use Heron's formula, let us solve first for the value of s via the equation
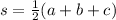
The lengths of the triangle are given in the problem. Just plug it in on the equation above and compute.
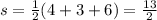
Now, let's move on using Heron's formula to solve the area of the triangle. We have
![\begin{gathered} A=\sqrt[]{s(s-a)(s-b)(s-c)} \\ A=\sqrt[\square]{(13)/(2)((13)/(2)-4)((13)/(2)-3)((13)/(2)-6)_{}} \\ A=\sqrt[]{(13)/(2)\lbrack((5)/(2)*(7)/(2)*(1)/(2))\rbrack} \\ A=\sqrt[]{(13)/(2)((35)/(8))} \\ A=\sqrt[]{(455)/(16)}=5.33 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/high-school/qlkf2qfg07p9i1rmvorv8zlqiwzntixn6e.png)
Therefore, the area of the triangle is 5.3 square units.