We can use the following definiotions to find our examples:
• An arc whose measure is less than 180 degrees is called a ,minor arc,.
,
• An arc whose measure is greater than 180 degrees is called a ,major arc,.
,
• An arc whose measure equals 180 degrees is called a ,semicircle,, since it divides the circle in two.
In this circle a major arc can be identified as BAD. We include the point A in the middle to indicate that the arc pass through it.
We can find its measure as:
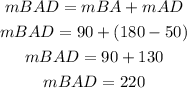
A minor arc can be expressed as BD. Its measure will be equal to:
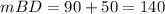
We can see that the sum of this two arc measures will be equal to the full circle measure (360°).
A semicircle can be identified as AC, and by definition will have a measure of 180°.
Then, we can complete the table as: