Given that
![\cot (\theta)=-\frac{\sqrt[]{35}}{7}](https://img.qammunity.org/2023/formulas/mathematics/college/nfxo8cg0pl94ihiw233kg7ij68ahpz21qb.png)
Note:
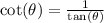
Therefore,
![(1)/(\tan (\theta))=-\frac{\sqrt[]{35}}{7}](https://img.qammunity.org/2023/formulas/mathematics/college/m01i89luq7ham8s9czqvhb2g4hnnjh1de3.png)
Cross-multiply
![\begin{gathered} 7*1=-\sqrt[]{35}*\tan (\theta) \\ 7=-\sqrt[]{35}\tan (\theta) \\ -\frac{7}{\sqrt[]{35}}=\tan (\theta) \\ \therefore\tan (\theta)=-\frac{7}{\sqrt[]{35}} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/hxzso6a6u8z7k86s3n7dj591rhofwqwhuo.png)
Using trigonometry ratios,
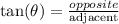
Where,
![\begin{gathered} \text{opposite}=-7 \\ \text{adjacent}=\sqrt[]{35} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/vtq65hfagfmcbt9boyzkwfzxitgj6rx0qf.png)
Let us now use Pythagoras theorem to obtain the hypotenuse
The formula for the Pythagoras theorem is,
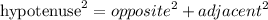
Hence,
![\begin{gathered} \text{hypotenuse}^2=(-7)^2+(\sqrt[]{35})^2 \\ \text{hypotenuse}^2=49+35=84 \\ \text{hypotenuse}=\sqrt[]{84}=\sqrt[]{4*21}=\sqrt[]{4}*\sqrt[]{21}=2*\sqrt[]{21}=2\sqrt[]{21} \\ \therefore\text{hypotenuse=}2\sqrt[]{21} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/hn6sow6n06yqax9m8bnrqd23duji1vtp0v.png)
We are to solve for csc(θ),
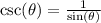
Where,
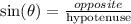
Hence,
![\sin (\theta)=-\frac{7}{2\sqrt[]{21}}](https://img.qammunity.org/2023/formulas/mathematics/college/uyfbf4oevrehb1lk9z2d4offwfm47723ae.png)
Therefore,
![\begin{gathered} \csc (\theta)=\frac{1}{-\frac{7}{2\sqrt[]{21}}} \\ \csc (\theta)=1/-\frac{7}{2\sqrt[]{21}} \\ \csc (\theta)=1*-\frac{2\sqrt[]{21}}{7}=-\frac{2\sqrt[]{21}}{7} \\ \therefore\csc (\theta)=-\frac{2\sqrt[]{21}}{7} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wxj8b2w6mmvr9qjjh3l892jmhul5wumiey.png)
Hence, the answer is
![\csc (\theta)=-\frac{2\sqrt[]{21}}{7}](https://img.qammunity.org/2023/formulas/mathematics/college/t8wzrwtepkcpl89aflfty0k0wa081b5uoj.png)