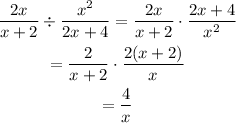a. Consider the expression
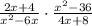
Use the property
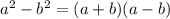
and cancel out the common terms in the numerator and denominator to simplify.
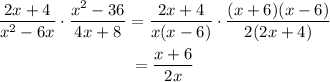
b. Consider the expression
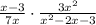
Factorize and cancel out the common terms in the numerator and denominator to simplify.
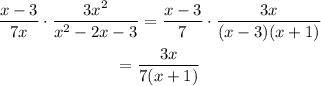
c. Consider the expression
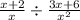
Cross multiply and cancel out the common terms in the numerator and denominator to simplify.
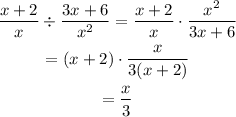
d. Consider the expression
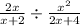
Cross multiply and cancel out the common terms in the numerator and denominator to simplify.