Question

During a science experiment, thetemperature of a liquid in a beaker started at8°C and dropped by 0.8°C every 2 minutes.Which function models the temperature ofthe liquid, y, after x minutes?

Answer 1

The Solution.

From the statement; the temperature of a liquid in a beaker started at 8 degrees Celcius, implies that the value of y is 8 when x = 0. That is, y-intercept is 8 degrees Celcius.

A drop of 0.8 degrees Celcius in every 2 minutes, implies the slope is as below:

`\text{slope =}(-0.8)/(2)=-0.4`

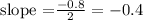
The function model is given as below:

`\begin{gathered} y=mx+c \\ \text{where m = slope = -0.4} \\ c=y-\text{intercept = 8} \end{gathered}`

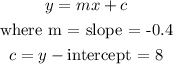
Substituting these values in the function model above, we get

`\begin{gathered} y=-0.4x+8 \\ or \\ y=8-0.4x \end{gathered}`

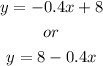
Thus, the correct answer is y = 8 - 0.4x (option B)