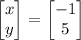First, write the matrix equation that represents the given system:
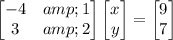
If we multiply both sides by the inverse of the coefficient matrix, we get:
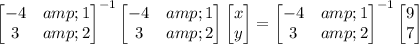
On the left member, the first two matrix factors cancel out. On the right member, find the explicit form of the inverse matrix:
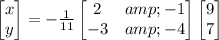
Remember that this rule can be used for finding the inverse of a 2x2 matrix:
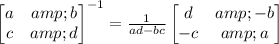
Next, perform the matrix product on the right member of the equation:
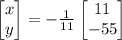
Finally, multiply the matrix on the right member by its coefficient of -1/11: