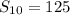Question

The first three terms of an arithmetic sequence are 8, 9, 10, What's the sum of the first ten terms of the series?A) 94B) 143C) 125D) 108

Answer 1

The sum of the first ten terms of the AP is;

`S_(10)=125`

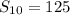
Step-by-step explanation:

Given the arithmetic sequence;

`8,9,10,\ldots`

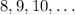
The first term is;

`a=8`

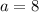
The common difference is;

`\begin{gathered} d=9-8 \\ d=1 \end{gathered}`

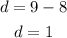
Recall that the sum of n terms of an AP can be calculated using the formula;

`S_n=(n)/(2)(2a+(n-1)d)`

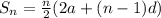
For the first ten terms;

`n=10`

Substituting the given values;

`\begin{gathered} S_(10)=(10)/(2)(2(8)+(10-1)1) \\ S_(10)=5(16+9) \\ S_(10)=5(25) \\ S_(10)=125 \end{gathered}`

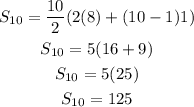
Therefore, the sum of the first ten terms of the AP is;

`S_(10)=125`