Given the below function
f(x) = -2(0.5)^x
Domain: 0, 1 ,2
Let the value of the domain = x
To find the function, substitute the value of into the above function
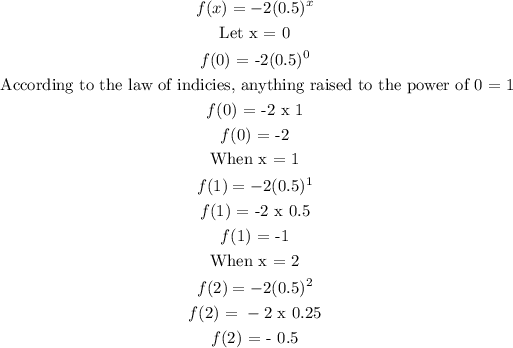
From the above solution, we can now draw out our table
x 0 1 2
f(x) -2 -1 -0.5
Let us graph the above pairs