Question

Evaluate the logarithm.(Can you give me a detailed step-by-step process of explaining how you evaluated. Also how a log works in general)

Answer 1

Given:

`log_2(512)`

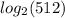
To solve it, follow the steps below.

Step 01: Use the given hint (512 = 32*16).

`log_2(32*16)`

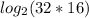
Step 02: Use the product rule for logarithms.

According to the product rule:

`log(a*b)=loga+logb`

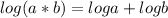
Then,

`log_2(32*16)=log_232+log_216`

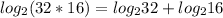
Step 03: Use the definition of the log to solve the problem.

Given the definition:

`log_ba=c\Leftrightarrow b^c=a`

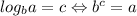
So, let's solve each part of the equation.

`log_232=x\Leftrightarrow2^x=32`

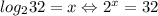
In order to find x, let's factor 32.

32 | 2

16 | 2

8 | 2

4 | 2

2 | 2

1

2⁵ = 32

`\begin{gathered} 2^x=2^5 \\ Then, \\ x=5 \end{gathered}`

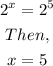
And,

`log_232=5`

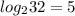
Now, let's solve the second term.

`\begin{gathered} log_216=y\Leftrightarrow2^y=16 \\ \end{gathered}`

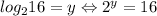
Let's factor 16:

16 | 2

8 | 2

4 | 2

2 | 2

1

2⁴ = 16

Substituting it in the equation:

`\begin{gathered} 2^y=2^4 \\ Since\text{ }the\text{ }bases\text{ }are\text{ }the\text{ }same,\text{ }the\text{ }exponents\text{ }must\text{ }be\text{ }the\text{ }same\text{ }too \\ y=4 \end{gathered}`

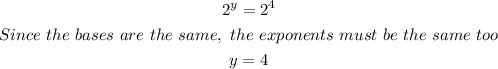
Then,

`log_216=4`

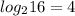
Step 04: Substitute the solutions and solve the equations.

`\begin{gathered} log_232=5 \\ log_216=4 \\ Then, \\ log_232+log_216=5+4 \\ =9 \end{gathered}`

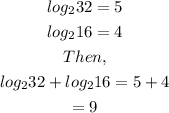
Answer: 9.