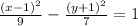Question

Find the equation of the hyperbola with the following properties. Express your answer in standard form.Foci at (-3, - 1) and (5, -1)Vertices at (-2, - 1) and (4, -1)

Answer 1

Given:

Foci: (-3, -1) and (5, -1)

Vertices: (-2, -1) and (4, -1).

Find: equation of the hyperbola in standard form

Solution:

As we can see in the coordinates of both its foci and vertices, they all lie on the same y-coordinate which is at -1. Therefore, the transverse axis of this hyperbola is parallel to the x-axis.

The pattern of the equation of the hyperbola in standard form parallel to the x-axis is:

`((x-h)^2)/(a^2)-((y-k)^2)/(b^2)=1`

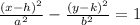
where (h, k) is the center of the hyperbola.

Now, to determine the center of the hyperbola, we use the coordinates of the vertices. The center of the hyperbola is located at the center of the two vertices.

Between x = -2 and x = 4, the center is 1. Hence, the center of the hyperbola is located at (1, -1). Hence, h = 1 and k = -1.

In a hyperbola, "a" is the distance from the center to the vertex. The distance between 1 and 4 is 3. Therefore, the value of "a" is 3.

In a hyperbola, "c" is the distance from the center to the focus. The distance between 1 and 5 is 4. Therefore, the value of "c" is 4.

To determine the value of "b", we can use the formula below:

`b=√(c^2-a^2)`

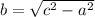
Let's replace "a" and "c" in the formula with the values that we have calculated.

`\begin{gathered} b=√(4^2-3^2) \\ b=√(16-9) \\ b=√(7) \end{gathered}`

Therefore, the value of "b" is √7.

Going back to the pattern of the equation of the hyperbola in standard form, let's plug in the value of h = 1, k = -1, a = 3, and b = √7.

`((x-1)^2)/(3^2)-((y-(-1))^2)/((√(7))^2)=1`

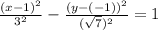
Then, simplify.

The standard equation of the hyperbola with the given properties is:

`((x-1)^2)/(9)-((y+1)^2)/(7)=1`