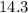Solution:
Given the figure:
To find the angle θ, we have
step 1: Find angle A.
Thus, we have
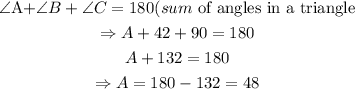
step 2: In the triangle ABC, solve for θ, using the sine rule.
Thus, we have
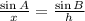
By substitution, we have
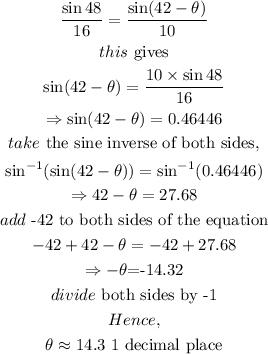
Hence, the angle of elevation of the ground, to 1 decimal place, is