Question

The equations of three lines are given below.Line 1: 2y-3x +42Line 2: y=-(2/3)x-7Line 3: 6x-4y=-2For each pair of lines, determine whether they are parallel, perpendicular, or neither.Line 1 and Line 2:O ParallelO Perpendicular ONeitherХhtLine 1 and Line 3:O ParallelO Perpendicular ONeitherLine 2 and Line 3: O ParallelO Perpendicular O Neither

Answer 1

Given three lines,

`\begin{gathered} 2y-3x+4=0 \\ y=-(2)/(3)x-7 \\ 6x-4y=-2 \end{gathered}`

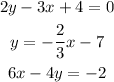
Re- writing the above equations of the form, y=mx+c,

`\begin{gathered} y=(3)/(2)x-2 \\ y=-(2)/(3)x-7 \\ y=(3)/(2)x+(1)/(2) \end{gathered}`

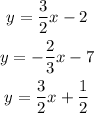
Here the slope are as follows,

`\begin{gathered} m_1=(3)/(2) \\ m_2=-(2)/(3) \\ m_3=(3)/(2) \end{gathered}`

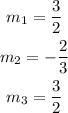
Since,

`m_1m_2=-1`

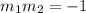
Line 1 and line 2 are perpendicular to each other.

`m_1=m_3=(3)/(2)`

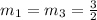
Therefore, line 1 and line 3 are parallel to each other.

`m_2m_3=-1`

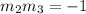
Line 2 and line 3 are perpendicular to each other.