Answer:
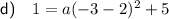
Explanation:

Given information:
- Vertex = (2, 5)
- Point on the parabola = (-3, 1)
Therefore:
To find the constant "a", substitute found values into the vertex formula:
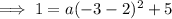
Additional information
Solve the equation for a:

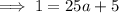

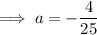
Therefore, the equation of the parabola in vertex form is:
