Question

Find the average rate of change on the following equation on the given interval. y=x^2+x+2 on [1,4]

Answer 1

The function is given as,

`y=x^2+x+2`

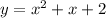
The interval is given as,

`\lbrack1,4\rbrack`

Consider that the average rate of change of a function f(x), in the interval [a,b] is given by,

`r=(f(b)-f(a))/(b-a)`

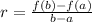
According to the given problem,

`\begin{gathered} f(x)=x^2+x+2 \\ a=1 \\ b=4 \end{gathered}`

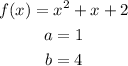
The value of the function at the end-points is calculated as,

`\begin{gathered} f(b)=f(4)=4^2+4+2=16+6=22 \\ f(a)=f(1)=1^2+1+2=1+3=4 \end{gathered}`

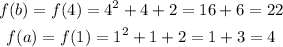
Substitute the values and simplify,

`\begin{gathered} r=(22-4)/(4-1) \\ r=(18)/(3) \\ r=6 \end{gathered}`

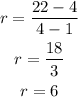
Thus, the average rate of change of the function is 6 units.