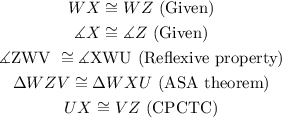Question

Can you tell me what the reasoning would be in this problem! This is proofs and I’m pretty sure the guy did the statement and reasoning wrong

Answer 1

Given the following figure:

We know that:

`\begin{gathered} WX\cong WZ \\ \measuredangle X\cong\measuredangle Z \end{gathered}`

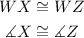
As we can see from the figure, both triangles ΔWZV and ΔWXU share the same angle ∡W, so we can say that:

`\measuredangle\text{ZWV }\cong\measuredangle\text{XWU}`

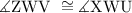
Separating the triangles:

Now, using the Angle-Side-Angle theorem, we can conclude that ΔWZV and ΔWXU are congruent:

`\Delta WZV\cong\Delta WXU`

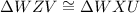
Finally, using the fact that the corresponding parts of congruent triangles are congruent (CPCTC), we can say that UX and VZ are congruent, since both are the opposite side of the congruent angle ∡W:

`UX\cong VZ`

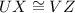
Summarizing:

`\begin{gathered} WX\cong WZ\text{ (Given)} \\ \measuredangle X\cong\measuredangle Z\text{ (Given)} \\ \measuredangle\text{ZWV }\cong\measuredangle\text{XWU (Reflexive property)} \\ \Delta WZV\cong\Delta WXU\text{ (ASA theorem)} \\ UX\cong VZ\text{ (CPCTC)} \end{gathered}`