Given the right triangle on the picture, line "x" is the altitude of the triangle and divides it into two smaller right triangles:
To determine the values of x, y, and z, the first step is to calculate the value of x.
As mentioned before, x is a perpendicular line that links the vertex of the right angle with the hypothenuse and divides the triangle into two similar right triangles. By definition, the relationship between the altitude and the two segments of the hypothenuse is the following:
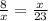
From this expression, you can determine the value of x:
-Multiply both sides of the equal sign by x, to take the term off the denominators place:
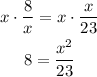
-Multiply both sides of the equal sign by 23, to cancel the division on the x-term:
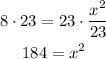
-Apply the square root to both sides of the expression to determine the value of x:
![\begin{gathered} \sqrt[]{184}=\sqrt[]{x^2} \\ 2\sqrt[]{46}=x \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/23pr1tlg2uq2q78c6t9exvjtkqt6jb0inv.png)
The value of x is 2√46
Both y and z are the hypothenuse of the right triangles formed by line x, considering that you know the length of the legs of the triangles, you can apply the Pythagorean theorem to calculate both side lengths.
The Pythagorean theorem states that the square of the hypothenuse is equal to the sum of squares of the legs of the triangle following the formula:

For the triangle on the left, which I named triangle I:
Hypothenuse c= y
Sides: a= 2√46
b= 8
You can determine the value of y as follows:
![\begin{gathered} (2\sqrt[]{46})^2+8^2=y^2 \\ 184+64=y^2 \\ 248=y^2 \\ \sqrt[]{248}=\sqrt[]{y^2} \\ 2\sqrt[]{62}=y \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/2klllsksn1xqhggyk3tw703p63xnx2edne.png)
For the triangle on the right, which I named triangle II:
Hypothenuse c=z
Sides
a= 2√46
b=23
You can determine the value of z as follows:
![\begin{gathered} (2\sqrt[]{46})^2+23^2=z^2 \\ 184+529=z^2 \\ 713=z^2^{} \\ \sqrt[]{713}=\sqrt[]{z^2} \\ \sqrt[]{713}=z \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/tyj0zju76x3ipnmmfzpjrc8nuoxz88enp3.png)
So the missing values are:
![\begin{gathered} x=2\sqrt[]{46} \\ y=2\sqrt[]{62} \\ z=\sqrt[]{713} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/8cc9f2wln11rp8vmabpzi9qfjm9x7twt2h.png)