Question

Section 5.2 Problem 10:

Find the general solution.

`y'' + 6y' + 13y = 0`
​

Answer 1

`y(x)=e^(-3x)[C_1cos(2x)+C_2sin(2x)]`

Explanation:

To solve a second-order homogeneous differential equation, we need to substitute each term with the auxiliary equation
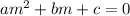`am^2+bm+c=0` where the values of
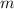`m` are the roots:

`y''+6y'+13y=0\\\\m^2+6m+13=0\\\\m^2+6m+13-4=0-4\\\\m^2+6m+9=-4\\\\(m+3)^2=-4\\\\m+3=\pm2i\\\\m=-3\pm2i`

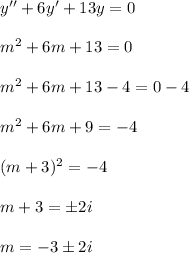
Since the values of
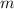`m` are complex conjuage roots, then the general solution is
`y(x)=e^(\alpha x)[C_1cos(\beta x)+C_2sin(\beta x)]` where
`m=\alpha \pm \beta i`.

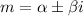Thus, the general solution for our given differential equation is
`y(x)=e^(-3x)[C_1cos(2x)+C_2sin(2x)]`.