Question

A. What is the complex conjugate of the denominator? Justify your reasoning!B. What mistakes did Melissa make while simplifying?Mistake 1:Mistake 2:Mistake 3:C. What is the correct solution to the problem? Show your work!D. What is the real part of the solution? What is the imaginary part?

Answer 1

The given equation is:

`(5+3i)/(1-4i)`

A) Complex conjuagte of the denominator = 1 + 41

The complex conjugate of an expression is the opposite of the sign between the real and imagiary parts

The denomiator in this case is 1 - 4i, the complex conjugate is therefore 1 + 4i

B) The mistakes made by Melissa:

Mistake 1: Melissa said i² = -i, this is wrong. i² = -1

Mistake 2: In the numerator, (5+3i)(1+4i) gave Melissa 5 + 12i², this is wrong.

(5+3i)(1+4i) = 5 + 20i + 3i + 12i² = 5 + 23i + 12(-1) = 5 - 12 + 23i

(5+3i)(1+4i) = -7 + 23i

Mistake 3: In the denominator, (1 - 4i)(1+4i) gave Melissa 16i + 1, this is wrong.

(1 - 4i)(1+4i) = 1 + 4i - 4i - 16i² = 1 - 16i² = 1 - 16(-1) = 1 + 16

(1 - 4i)(1+4i) = 17

c) The correct solution of the problem:

`(5+3i)/(1-4i)`

Step 1: Rationalise, that is multiply the numerator and the denominator by the conjugate of 1 - 4i, the conjugate is 1 + 4i

`\begin{gathered} (5+3i)/(1-4i)*(1+4i)/(1+4i) \\ \text{Step}2\colon\text{ }(5+20i+3i+12i^2)/(1+4i-4i-16i^2) \\ \text{Step}3\colon\text{ }(5+23i+12(-1))/(1-16(-1)) \\ \text{Step}4\colon\text{ }(-7+23i)/(17) \\ \text{Step}5\colon\text{ }(-7)/(17)+(23)/(17)i \end{gathered}`
`\text{Answer: }(-7)/(17)+(23)/(17)i`

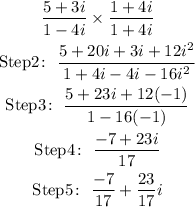
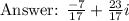
D) Real part = -7/17

Imaginary part = 23/17