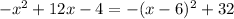The given equation is
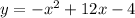
To complete the square take -1 as a common factor from the right side
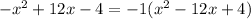
Divide the term of x by 2 to find the product of the first and second terms in the bracket
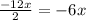
The bracket will be (x - 6)
Square it
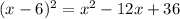
Then add and subtract (36 - 4)
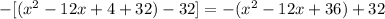
Make the trinomial a square binomial
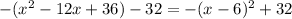
The completing square is