Question

I believe the y intercept is 8 (I think) please help me solve this algebra 2 please show steps as well so I can understand

Answer 1

b)

The function f(x) will be positive, in other words, f(x) > 0, when the result of all linear factors be positive, or, two negatives and one positive! Remember the rule of signals for multiplication:

`\begin{gathered} (+)\cdot(+)\cdot(+)=(+) \\ (-)\cdot(-)\cdot(+)=(+) \\ (+)\cdot(-)\cdot(-)=(+) \\ (-)\cdot(+)\cdot(-)=(+) \end{gathered}`

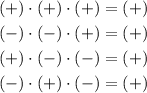
Then, if (2x-1) is positive, the other two linear factors must or both positive or both negative, and the function f(x) will be positive as well.

Let's analyze when each linear factor is positive:

First linear factor

`\begin{gathered} 2x-1>0 \\ \\ x>(1)/(2) \end{gathered}`

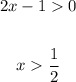
Second linear factor

`\begin{gathered} x+4>0 \\ \\ x>-4 \end{gathered}`

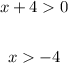
Third linear factor

`\begin{gathered} x-2>0 \\ \\ x>2 \end{gathered}`

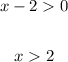
Let's make a table to help us!

As we can look at our table, the interval where f(x) is positive is

`-42`

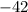
c)

Using the result on B, we can see that for any value of x < -4, the function will be negative, then it will only grow negatively! Then we can say that

`x\rightarrow-\infty,f(x)\rightarrow-\infty`

And for x > 2, the function will grow positive! then we can also say that

`x\rightarrow\infty,f(x)\rightarrow\infty`

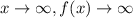
This leads us to the letter C as correct answers:

`x\rightarrow-\infty,f(x)\rightarrow-\infty\text{ and as }x\rightarrow\infty,f(x)\rightarrow\infty`

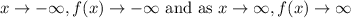
d)

Using the results on B again, we can see that the function was negative before -4, goes positive, goes negative again on 1/2, goes positive on 2 and it will be positive forever. The special aspect here is the fact that the function was negative, goes positive, and goes negative again, like:

Then we can say that the function has one relative maximum and one relative minimum!