Let l be the length of the longer leg, s be the length of the shorter leg, and h be the length of the hypotenuse, then we can set the following equations:
![\begin{gathered} l=s+7cm\text{.} \\ h=s+9\operatorname{cm}\text{.} \end{gathered}]()
Using the Pythagorean theorem we get:
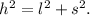
Substituting the first and second equation in the above one we get:
![(s+9cm)^2=(s+7\operatorname{cm})^2+s^2\text{.}]()
Solving for s we get:
![\begin{gathered} s^2+s\cdot18\operatorname{cm}+81\operatorname{cm}=s^2+s\cdot14\operatorname{cm}+49\operatorname{cm}^2+s^2, \\ s\cdot18\operatorname{cm}+81\operatorname{cm}^2=s^2+s\cdot14\operatorname{cm}+49\operatorname{cm}^2, \\ s^2-s\cdot4\operatorname{cm}-32\operatorname{cm}^2=0, \\ (s-8\operatorname{cm})(s+4\operatorname{cm})=0, \\ s=8\operatorname{cm}. \end{gathered}]()
Substituting s=8cm in the first and second equation we get:
![\begin{gathered} l=8\operatorname{cm}+7\operatorname{cm}=15\operatorname{cm}, \\ h=8\operatorname{cm}+9\operatorname{cm}=17\operatorname{cm}\text{.} \end{gathered}]()
Answer:
Length of the shorter leg: 8cm.
Length of the longer leg: 15cm.
Length of the hypotenuse: 17cm.