f(x) is undefined for all x < 0.
Hence, the domain of f is [0, ∞)
![f(0)=\sqrt[]{0^2+6(0)}-(0)=0](https://img.qammunity.org/2023/formulas/mathematics/college/osv925c14d1l7e0e3zx8dvea2rurzjobpi.png)
Hence, the y-intercept is 0
When f(x) = 0
![\begin{gathered} \sqrt[]{x^2+6x}-x=0 \\ \sqrt[]{x^2+6x}=x \\ \text{ Squaring both sides, we have} \\ x^2+6x=x^2 \\ \text{Hence} \\ 6x=0 \\ (6x)/(6)=(0)/(6) \\ \text{Thus x = 0} \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/dkantyaz3k0toi3b7obkm36bowooafn4up.png)
Hence, the x-intercept is also 0
The image of the graph is as shown below
From the image of the graph, we can see that there is no apparent symmetry
![\begin{gathered} f(x)=\sqrt[]{x^2+6x}-x \\ \text{ Therefore,} \\ f^(\prime)(x)=(1)/(2)*(2x+6)(x^2+6x)^{-(1)/(2)}-1 \end{gathered}](https://img.qammunity.org/2023/formulas/mathematics/college/wqmb7fseqpcjinoj0mi2uxugf5pf3etquh.png)
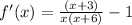
Therefore.
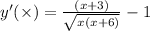
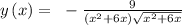
From the graph, we can see that there is no vertical asymptote,
But there is a horizontal asymptote, y = 3
The graph f(x) is increasing for f'(x) > 0

From the image, we can see that the function is increasing on the interval [0, ∞ )