The initial velocity of the skateboard, u=0 m/s
The length of the ramp, s=15.0 m
The angle of inclination, θ=20.0°
The time duration, t=3.00 s
The final velocity of the skateboard, v=10.0 m/s
The acceleration due to gravity, g=9.81 m/s²
Let us calculate gsinθ
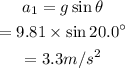
From the equation of the motion,
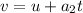
Where a₂ is the acceleration of the skateboard.
On substituting the known values,

On comparing we find that,
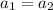
Thus, the acceleration of the skateboard is g sinθ.