we calculate the vinegar on 220 ml
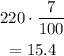
the dressing will have 15.4 ml of vinegar
now we can raise a sum
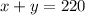
where X is the first brand and Y the second brand on ml
now the percent vinegar sum we know the result is 15.4 wich corresponds to 7%
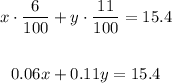
we have two unknowns and equations, so we can solve by any method.
i will solve y on the first equation
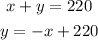
and replace on the second to find x
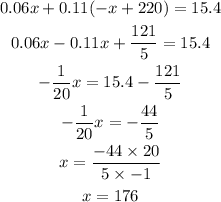
then replace x on any equation to solve y
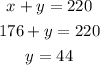
for each brand should she use x=176ml and y=44ml